Nel III secolo a.C. un dotto greco di nome Eratostene (e. 276-c. 195 a.C.) esegui la prima misurazione nota delle dimensioni della Terra. Gli strumenti di cui si servì in quest'impresa erano molto semplici: l'ombra proiettata dallo gnomone di una meridiana, più una serie di misurazioni e di assunti. La determinazione della circonferenza terrestre fu però così ingegnosa che sarebbe stata citata con ammirazione per molti secoli. L'esperimento di Eratostene è così semplice e istruttivo che viene ripetuto ogni anno, quasi 2500 anni dopo, da studenti di tutto il mondo. E il principio è così elegante che, dopo averlo capito, ti viene quasi voglia di andare a misurare la lunghezza di un'ombra.
L'esperimento di Eratostene combinò due idee di grande importanza. La prima fu quella di raffigurare ìl cosmo come un insieme di oggetti (la Terra, il Sole, i pianeti e le stelle) nel comune spazio tridimensionale. Ciò può sembrare ovvio a noi, ma non lo era affatto al tempo di Eratostene; la tesi che sotto la miriade di moti sempre mutevoli nel mondo e nel cìelo notturno ci fosse un ordine impersonale e immutabile, un'architettura che poteva essere descritta e spiegata dalla geometria fu un contributo importante dato dai greci alla scienza. La seconda idea fu quella di applicare comuni attività di misurazione alla comprensione della vastità e delle dimensioni di quest'architettura cosmica. Combinando queste due idee, Eratostene escogitò l'audace nozione che le stesse tecniche che erano state sviluppate per costruire case e ponti, per tracciare campi e strade e prevedere inondazioni e monsoni potessero fornire informazioni sulla grandezza della Terra e di altri corpi celesti.
Eratostene suppose prima di tutto che la Terra fosse approssimativamente sferica. Infatti, nonostante la convinzione oggi piuttosto diffusa che Colombo, partendo per la sua impresa, intendesse dimostrare che il mondo non era piatto, molti fra gli antichi greci che avevano riflettuto profondamente sul cosmo avevano già concluso che la Terra non solo doveva essere sferica, ma doveva anche essere relativamente piccola a paragone col resto dell'universo. Fra quei pensatori c'era Aristotele, il cui libro De caelo, scritto un secolo circa prima di Eratostene, propose vari argomenti, alcuni dei quali logici e altri empirici, a sostegno della tesi che la Terra doveva essere sferica. Aristotele sottolineò, per esempio, che durante le eclissi di Luna l'ombra della Terra proiettata su di essa aveva sempre un contorno circolare. Notò anche che i viaggiatori, quando percorrono grandi distanze verso nord o verso sud, vedono stelle diverse (cosa che non avverrebbe se la Terra fosse piatta), che certe stelle visibili in Egitto e a Cipro non sono più visibili nei paesi più settentrionali, e che certe altre stelle sempre visibili nei paesi nordici sorgono e tramontano nel Sud, come se fossero viste dalla superfìcie di un oggetto sferico. « Argomentando sulla base di tutti questi elementi, abbiamo non solo che la mole della Terra risulta di necessità sferica, ma anche che essa non è grande, se la si raffronta alle dimensioni degli altri astri. »
Ma il grande pensatore offrì anche argomenti più creativi. Da relazioni di viaggiatori in paesi stranieri e di spedizioni militari, sapeva che gli elefanti si trovavano in paesi lontani, ai due estremi del mondo conosciuto: a ovest (in Africa) e a est (in Asia). «E questo accadrebbe in quanto i due estremi si toccano »: una congettura abile anche se sbagliata. Altri studiosi greci aggiunsero ulteriori argomenti a sostegno della forma sferica della Terra, compresa la differenza nell'ora del sorgere e tramontare del Sole in diversi paesi, e il fatto che si continua a vedere l'alberatura delle navi che si allontanano dalla costa quando le navi stesse sono già scomparse sotto l'orizzonte.
Nessuno di questi argomenti rispondeva però a una domanda fondamentale: quanto è grande questa Terra sferica? Non era possibile conoscerne la grandezza senza che qualcuno ne misurasse un passo dopo l'altro l'intera circonferenza? Fino a Eratostene sappiamo solo di stime della grandezza della Terra. La più antica che conosciamo si trova in Aristotele, il quale scrisse che «i matematici che tentano di computare la lunghezza della circonferenza terrestre, dicono che essa è di circa 400.000 stadi », ma egli non ci rivela né le sue fonti né il ragionamento su cui si fondavano tali stime. E inoltre impossibile convertire esattamente tale cifra in unità moderne. Uno «stadio» - misura che si riferisce alla lunghezza di una pista greca per le corse di atletica - variava da una città all'altra. Usando una rozza stima per la misura dello stadio, i ricercatori attuali hanno ipotizzato che il valore fornito da Aristotele fosse pari a un po' più di 40.000 miglia (64.360 km, contro i circa 40.000 km reali). Archimede, che costruì modelli del cosmo in cui i corpi celesti ruotavano l'uno intorno all'altro, formulò una stima un po' minore di quella di Aristotele: 30.000 stadi, ossia più di 48.000 km. Anche lui, però, non fornì alcun indizio circa la fonte del suo ragionamento.
Entra ora in scena Eratostene. Contemporaneo più giovane di Archimede, era nato in Nordafrica, a Cirene, e aveva studiato ad Atene. Era un erudito enciclopedico, esperto in molte aree della cultura, dalla critica letteraria e dalla poesia alla geografìa e alla matematica. Non si pensava però che avesse raggiunto il massimo livello in nessuna, cosa che spiega perché i suoi colleghi gli avessero attribuito il soprannome sarcastico di « Beta », la seconda lettera dell'alfabeto greco, in un gioco di parole che significava che egli era il secondo in tutto. Nonostante le irrisioni, la sua fama era così grande che alla metà del III secolo a.C. il re d'Egitto lo invitò a istruire suo figlio e in seguito lo nominò direttore della famosa biblioteca di Alessandria: la prima biblioteca e la più grande nel suo genere, fondata dai Tolomei, sovrani d'Egitto, nel corso della costruzione di Alessandria come capitale culturale del mondo greco. La biblioteca divenne un punto d'incontro per studiosi di tutto il mondo, e Alessandria diventò un importante crocevia culturale: per esempio, fu patria di Euclide e della sua scuola. Ad Alessandria i bibliotecari riuscirono a raccogliere una vasta collezione dì manoscritti su una vasta gamma di argomenti che chiunque avesse credenziali appropriate potesse usare. (La biblioteca di Alessandria fu anche la prima, a quanto sappiamo, a ordinare i manoscritti in ordine alfabetico per autore.)
Eratostene scrisse due opere di geografia considerate di grande importanza nel mondo antico. I Geographica, in tre libri, furono la prima opera a fornire carte geografìche dotate di paralleli (i cerchi paralleli all'equatore, la cui lunghezza diminuisce sempre più man mano che ci si avvicina ai poli) e di meridiani (i cerchi massimi che passano per entrambi i polì e per una posizione data). La sua Misurazione del mondo conteneva la prima descrizione nota di un modo per misurare la grandezza della Terra. Purtroppo entrambe le opere (ma forse la seconda faceva parte della prima) sono andate perdute, e noi abbiamo tentato di ricostruire il ragionamento di Eratostene a partire dalle osservazioni di altri autori antichi che le conobbero. Per fortuna furono in molti a conoscerle.
Eratostene cominciò il suo ragionamento dicendo che, se la Terra era un piccolo corpo sferico in un vasto universo, altri corpi, come il Sole, dovevano essere molto lontani, così lontani che i raggi dovevano essere essenzialmente paralleli dovunque colpissero la Terra. Sapeva anche che, man mano che il Sole saliva in ciclo, le ombre degli oggetti sulla Terra andavano progressivamente accorciandosi; aveva appreso da relazioni di viaggiatori che al solstizio d'estate nella cittadina di Siene (la moderna Assuan) il Sole si trovava a mezzogiorno esattamente allo zènìt (sulla verticale del luogo) e che le ombre di tutti gli oggetti verticali sparivano, comprese le colonne, i pali e persino gli gnomoni, gli indicatori verticali o stili nelle meridiane, la cui unica funzione era quella di proiettare ombre. Le ombre sembravano addirittura sparire dal pozzo della città quando la luce lo illuminava tutto uniformemente, « come un tappo che entra esattamente nell'imboccatura di una bottiglia», secondo una fonte antica. (Sto un po' esagerando: le ombre non sparivano -del tutto, ma semplicemente cadevano proprio sotto gli oggetti, anziché di lato come fanno di solito.) Eratostene sapeva anche che Alessandria era a nord di Siene e press'a poco sullo stesso meridiano. E grazie ai bematisti reali, che il governo egiziano mandava ogni anno a rimisurare a passi le terre e ad aggiornare le carte topografìche dopo l'inondazione stagionale del Nilo, sapeva che le due città distavano circa 5000 stadi l'una dall'altra (il numero era arrotondato cosicché non possiamo usare questo valore per stabilire un'equivalenza esatta fra stadi e unità moderne).
Per esprimerci in termini moderni, Siene si trovava sul Tropico del Cancro, una linea immaginaria parallela all'equatore (da cui dista circa 23,5° verso nord), che passa per il Messico settentrionale, l'Egitto meridionale, l'India e la Cina meridionale (e che è segnata sulla maggior parte dei mappamondi). Tutti i punti che giacciono sul Tropico del Cancro condivìdono un carattere inusuale: il Sole si trova esattamente a perpendicolo (a mezzogiorno) solo una volta all'anno, nel corso del giorno più lungo dell'anno, ossia il 21 giugno, solstizio d'estate. Le persone che vìvono a nord del Tropico del Cancro non hanno mai il Sole direttamente sulla verticale, e quindi il Sole proietta sempre un'ombra. Le persone che vivono nell'emisfero Nord ma a sud del tropico vedono il Sole direttamente allo zenit due volte all'anno, una volta prima del solstizio e una volta dopo (il giorno esatto dipende dalla loro posizione geografica). La ragione di ciò ha attinenza con la posizione della Terra, il cui asse è inclinato rispetto al Sole. Questo fatto, però, non preoccupò Eratostene. Quel che importava per lui era il fatto che, quando il Sole era direttamente sulla verticale a Siene, non sarebbe stato allo zenit in alcun altro luogo né a nord né a sud — compresa Alessandria —, luoghi nei quali uno gnomone avrebbe proiettato un'ombra. La lunghezza dell'ombra sarebbe dipesa dall'entità della curvatura della Terra: se la curvatura era grande, un'ombra proiettata in un luogo come Alessandria sarebbe stata più lunga che se la curvatura della Terra fosse stata piccola.
Grazie alla sua conoscenza della geometria, Eratostene sapeva abbastanza per escogitare un ingegnoso esperimento che gli avrebbe rivelato l'esatto ammontare della curvatura della Terra, e quindi la sua circonferenza. Per apprezzare la bellezza di questo esperimento, non c'è bisogno di sapere qualcosa sul modo specifico in cui procedette Eratostene. Questa è una fortuna, dal momento che non possediamo neppure la sua descrizione di quel che fece. Conoscìa-. mo il suo procedimento solo attraverso descrizioni incomplete di seconda mano lasciateci da suoi contemporanei e successori, la maggior parte dei quali, chiaramente, non ne capirono tutti i particolari. Noi non abbiamo bisogno dì sapere nulla sulla sua linea di ricerca: che cosa abbia motivato specificamente il suo interesse per questo problema, quali siano stati i suoi primi passi, quali gli eventuali ripensamenti, se ne ebbe, come raggiunse infine il suo obiettivo, e in quali altre direzioni tu poi condotto. E un peccato che sia così, perché possiamo trame l'impressione che l'idea gli sia venuta in conseguenza di un'intuizione isolata, un fulmine a ciel sereno, ma ciò non ci impedisce di capire l'esperimento. Non dobbiamo neppure impegnarci in grandi salti speculativi per seguire un complesso ragionamento matematico, o usare abili congetture empiriche fondate su cose come la demografìa degli elefanti. La bellezza di questo esperimento risiede nel modo in cui permette di scoprire una dimensione dì proporzioni cosmìche misurando la lunghezza di un'esile ombra.
La sua stupefacente semplicità ed eleganza può essere colta in due diagrammi. Durante il solstizio estivo, quando il Sole a mezzogiorno è direttamente allo zenit a Siene (A), le ombre scompaiono, ossia vengono proiettate direttamente verso il centro della Terra (lìnea AB). Nello stesso istante le ombre ad Alessandria (E) vengono proiettate nella stessa dirczione (CO), in quanto i raggi del Sole (data la sua grandissima distanza) sono praticamente paralleli; poiché però la superfìcie della Terra è curva, essi intersecano la superfìcie a un piccolo angolo, che chiameremo x. Un piccolo angolo o un'ombra corta significherebbero una Terra quasi piatta, con una lieve curvatura corrispondente a una circonferenza molto grande; un angolo grande o un'ombra lunga significherebbero una forte curvatura e una circonferenza relativamente piccola. C'era un modo per calcolare esattamente la circonferenza con la lunghezza delle ombre? La geometria si rivelò utile per risolvere questo problema.
Secondo Euclide, gli angoli alterni interni formati da una linea che interseca due parallele sono uguali. Così l'angolo (x) formato dalle ombre ad Alessandria è uguale all'angolo (y) creato dai due raggi con vertice al centro della Terra che passano per Alessandria e per Siene (BC e BA). Ciò significa a sua volta che il rapporto fra la lunghezza dell'arco di uno gnomone (FE) e il cerchio completo intorno allo gnomone è uguale al rapporto fra la distanza da Siene ad Alessandria (AE) e la circonferenza terrestre. Eratostene si rese quindi conto che, se si fosse misurata questa distanza, si sarebbe potuta calcolare la circonferenza terrestre.
Anche se non sappiamo in quale dei vari modi possibili Eratostene abbia compiuto le sue misurazioni, gli storici della scienza sono quasi certi che si sia servito della skaphe, la versione greca della meridiana. Questo antico orologio solare concavo era formato da una sorta dì catino o bacino, solitamente di bronzo, dotato di uno gnomone, la cui ombra, spostandosi lentamente nel corso della giornata, andava a toccare le varie linee orarie incise nella superfìcie del bacino. Eratostene usò però questo strumento in un modo nuovo. Egli non era interessato alla posizione dell'ombra sulle varie linee orarie per misurare il passaggio del tempo, bensì all'angolo formato dall'ombra proiettata dallo gnomone a mezzogiorno al solstizio d'estate. Egli misurava quell'angolo e determinava quale frazione esso fosse del cerchio completo (la pratica della misurazione dei gradi ottenuta dividendo un cerchio in 360 parti uguali sarebbe entrata in uso solo un secolo dopo). Oppure, con un procedimento che era diverso solo nella forma, avrebbe potuto misurare il rapporto della lunghezza dell'arco determinato dall'ombra dello gnomone sul bacino alla lunghezza totale della circonferenza del bacino.
A mezzogiorno, nel giorno del solstizio d'estate, Eratostene accertò che l'ombra solare ad Alessandria era inclinata di 1/50 di un cerchio completo (noi oggi diremmo di 7,2 gradi) rispetto alla verticale (ovvero rispetto alla posizione di Siene, dove la dirczione della verticale e quella dell'ombra coincidevano). La distanza fra Alessandria e Siene era quindi pari a un cinquantesimo della lunghezza dell'intero meridiano che più o meno passava per le due città. Moltiplicando 5000 stadi per 50, Eratostene ottenne per la circonferenza terrestre 250.000 stadi, che successivamente corresse a 252.000 (entrambe le misure corrispondono a poco più di 40.000 km). La ragione di questa correzione non è chiara, ma probabilmente c'entrava in qualche modo il desiderio di semplificare il calcolo delle distanze geo-grafiche. Eratostene aveva infatti l'abitudine di dividere i cerchi ìn 60 parti, e una circonferenza di 252.000 stadi divisa per 60 dava esattamente 4200 stadi. Ma sia che si usino per la circonferenza terrestre 250.000 o 252.000 stadi, e qualunque valore numerico si usi per convenire Ì suoi stadi in unità di lunghezza moderne, la stima di Eratostene supera solo di una piccola percentuale Ìl valore oggi in uso di 40.009 km (la lunghezza del meridiano, mentre la lunghezza dell'equatore è dì 40.077 km).
L'immagine del cosmo di Eratostene ebbe un'importanza determinante per il successo dell'esperimento. Senza tale particolare immagine, la misurazione dell'ombra non avrebbe potuto fornire la circonferenza terrestre. Per esempio, un antico testo cartografico cinese, lo Huainanzi, o « Libro del maestro dì Huainan », nota che gnomoni della stessa altezza ma a distanze diverse (nella dirczione nord-sud) l'uno dall'altro proiettano nello stesso tempo ombre di lunghezza diversa. Sulla base dell'assunto che la Terra è essenzialmente piatta, l'autore attribuì questa differenza al fatto che lo gnomone che proietta l'ombra più corta si trova più direttamente sotto il Sole, e sostenne che la differenza nella lunghezza delle ombre può essere usata per calcolare l'altezza del cielo!
I dati di Eratostene, e la sua misurazione, erano approssimati. Egli si rese probabilmente conto che Siene non sì trovava esattamente sul Tropico del Cancro, né esattamente a sud di Alessandria (sullo stesso meridiano). La distanza fra le due città non è inoltre esattamente di 5000 stadi. E poiché il Sole non è un punto di luce bensì un piccolo disco (di circa mezzo grado di diametro visuale apparente), la luce proveniente da un lato del disco non colpisce lo gnomone esattamente allo stesso angolo dì quella proveniente dall'altro lato, diffondendo lievemente l'ombra.
Data però la limitata tecnologia disponibile a Eratostene, si può dire che l'esperimento riuscì abbastanza bene. La sua misura di 252,000 stadi fu accettata per secoli dagli antichi greci come un valore attendibile per la circonferenza terrestre. Nel I secolo a.C. l'enciclopedista romano Plìnio il Vecchio elogiò Eratostene come « autorità eminente » sulla circonferenza della Terra, definendo il suo esperimento «audace», il suo ragionamento « sottile », e il valore numerico da lui trovato come « approvato da tutti». Un secolo circa dopo Eratostene, un altro dotto greco cercò di usare, per misurare la circonferenza terrestre, la differenza fra l'angolo della stella molto splendente Canopo visibile da Alessandria e l'angolo visibile da Rodi (dove si diceva che essa fosse appena discernibile proprio sull'orizzonte), ma Ìl risultato ottenuto fu inattendibile. Ancora un millennio dopo gli astronomi arabi furono incapaci di migliorare il risultato di Eratostene, anche se tentarono altri procedimenti, come misurare l'orizzonte della Terra come lo si vede dalla cima di una montagna di altezza nota, e misurare simultaneamente da due diverse località l'altezza di una stella sull'orizzonte. La misurazione di Eratostene non sarebbe stata migliorata fino ai tempi moderni, quando divennero possibili misurazioni molto più esatte delle posizioni dei corpi celesti.
L'esperimento di Eratostene trasformò la geografia e l'astronomia. Innanzitutto permise a qualsiasi geografo di stabilire la distanza fra due località di latitudine nota, per esempio fra Atene e Cartagine, o fra Cartagine e la foce del Nilo. Permise a Eratostene di calcolare grandezza e posizione del mondo abitato noto, e fornì ai suoi successori un metro per cercare di determinare altre dimensioni cosmiche, come le distanze da noi alla Luna, al Sole e alle stelle. In breve, l'esperimento di Eratostene trasformò l'immagine che gli uomini avevano della Terra, della posizione della Terra nell'universo (o almeno nel sistema solare) e del posto dell'uomo nell'universo.
(Tratto da "Il prisma e il pendolo" - Robert P. Crease - 2007 Longanesi)
 « ... Piantata un'asta al limite dell'ombra proiettata dalla piramide, poiché i raggi del sole, investendo l'asta e la piramide formavano due triangoli, [ha] dimostrato che l'altezza dell'asta e quella della piramide stanno nella stessa proporzione in cui stanno le loro ombre.» (Plutarco)
« ... Piantata un'asta al limite dell'ombra proiettata dalla piramide, poiché i raggi del sole, investendo l'asta e la piramide formavano due triangoli, [ha] dimostrato che l'altezza dell'asta e quella della piramide stanno nella stessa proporzione in cui stanno le loro ombre.» (Plutarco) 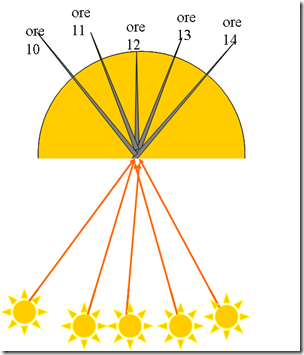 Talete voleva fare la misura a mezzogiorno. La latitudine di Giza, presso cui è situata la Grande Piramide, è di circa 30°, quindi perché l’inclinazione dei raggi a mezzogiorno sia di 45° occorre fare la misura 2 mesi prima o dopo l’equinozio.
Talete voleva fare la misura a mezzogiorno. La latitudine di Giza, presso cui è situata la Grande Piramide, è di circa 30°, quindi perché l’inclinazione dei raggi a mezzogiorno sia di 45° occorre fare la misura 2 mesi prima o dopo l’equinozio.