fisica facile

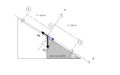
Un corpo di massa m=500 g, si trova, fermo, sulla sommità di un piano inclinato liscio di 45° rispetto all'orizzontale. Ad un certo istante viene lasciato libero di percorre sul piano una distanza di 20 m prima di entrare in una parte del piano scabra. Se il corpo si arresta dopo aver percorso altri 20 m sul piano inclinato scabro, calcolare quanto vale il coefficiente di attrito dinamico.

Soluzione.
Questo piano inclinato ha una parte liscia seguita da una parte scabra con attrito  m (che dobbiamo trovare).
Chiamiamo l il tratto percorso sulla parte liscia. Esso va dal punto (0) , punto di inizio del moto, al punto (1), punto di ingresso nella zona scabra. Il punto (2) poi corrisponde al momento in cui il corpo si ferma, sottoposto alla forza d'attrito dinamico che è contraria al verso del moto (decelerazione). La distanza tra i punti (1) e (2) è pure essa l.

Fissiamo l'asse X lungo il piano inclinato con verso a scendere. non è difficile vedere (figura) che il dislivello h tra i punti (0) ed (1) sia proprio h = l sin α
per cui la velocità di arrivo nel punti (1) sarà
v₁ = √ (2 g h) = √ (2 g l sin α)
Lungo la parte scabra possiamo applicare il teorema dell'energia cinetica, calcolando il lavoro svolto dalla forza totale lungo l'asse X nel tratto 1-2. Questo lavoro sarà uguale alla differenza tra l'energia cinetica nel punto 2 e l'energia cinetica nel punto 1.
La forza totale lungo l'asse X e data dalla somma della componente X della forza peso che è F_px = mg sin α, più la forza d'attrito F_a = - m N = - m mg cos α.
Quindi F_tot,x = mg (sin α - m cos α)
Il lavoro sul tratto 1-2 sarà il prodotto scalare della forza totale per lo spostamento l effettuato:
L(1 - 2) = F_tot,x • l = mg (sin α - m cos α) l 
che, per il teorema suddetto  sarà appunto uguale a
E_c(2) - E_c(1) = 0 - 1/2 m v₁², ricordate che nel punto 2 il corpo si ferma, quindi Ec = 0.
Quindi  m g l (sin α - m cos α) = - 1/2 m 2 g l sin α
Con un po di semplificazioni otteniamo:
sin α - m cos α = - sin α    
m cos α = 2 sin α   
m = 2 tg α = 2 tg 45° = 2.