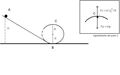
Supponiamo di avere un piano inclinato liscio sul quale possa scorrere senza attrito una biglia metallica. Alla base del piano sia posta in verticale una guida circolare priva di attrito di raggio R = 40 cm (vedi figura).
Da quale altezza H sul piano inclinato deve partire la biglia per poter percorrere un giro completo nella guida circolare?
Soluzione.
Questo tipo di problema può essere risolto con la legge di conservazione dell'energia meccanica, in quanto l'unica forza in gioco (responsabile del moto della biglia) è la forza peso che è conservativa e non sono presenti attriti vari.
Cominciamo col calcolare la velocità alla base del piano inclinato supponendo di porre la biglia ad un'altezza generica H:
nel punto A (segnato in figura) abbiamo
energia potenziale Ep(A) = mgH
energia cinetica Ec(A) = 0 --> la biglia parte da ferma!
nel punto B (segnato in figura) abbiamo:
energia potenziale Ep(B) = 0 --> siamo al suolo!
energia cinetica Ec(B) = ½ m V B2
allora dalla conservazione dell'energia meccanica (somma di En cinetica ed En potenziale) si avrà :
Ep(A) + Ec(A) = Ep(B) + Ec(B)
mgH = ½ m V B2
ora eliminando m e moltiplicando per 2 in ambo i membri dell'ultima uguaglianza, otteniamo
V B2 = 2gH ed estraendo radice di ambo i membri trovo la velocità di arrivo al suolo:
V B = √ (2gH) --> un risultato ben noto!
VB è ora la velocità di ingresso nella ruota verticale, anch'essa priva di attrito. Possiamo ancora usare la conservazione dell'energia meccanica, ma prima va fatta una considerazione.
Affinche la biglia giunga nel punto più alto del cerchio (altezza 2R dal suolo), cioè il punto C (segnato in figura), essa in tale punto deve avere una velocità tale da non cadere in giù!
Si tratta di un moto "circolare", quindi per poter mantenere la biglia sulla guida la "reazione" dovuta alla forza centrifuga (diretta verso l'alto) dovrà essere uguale alla forza peso (diretta verso il basso)
m V C2 / R = m g
di nuovo eliminando m e portando R sopra a destra, trovo dopo aver estratto radice:
V C = √ (gR)
In sostanza questa è la velocità che "dovrebbe" possedere la biglia nel punto C per poter fare un giro completo!
Allora adesso passiamo alla conservazione dell'energia meccanica tra i punti B e C, considerando tale velocità per l'energia cinetica in C:
nel punto B (segnato in figura) abbiamo
energia potenziale Ep(B) = 0 --> siamo al suolo!
energia cinetica Ec(B) = ½ m V B2
nel punto C (segnato in figura) abbiamo:
energia potenziale Ep(C) = 2 m g R --> altezza dal suolo attuale = 2R
energia cinetica Ec(C) = ½ m V C2
allora dalla conservazione dell'energia meccanica (somma di En cinetica ed En potenziale) si avrà :
Ep(B) + Ec(B) = Ep(C) + Ec(C)
½ m V B2 = 2 m g R + ½ m V C2
possiamo cominciare a snellire l'equazione eliminando le masse e moltiplicando ambo i membri per 2
V B2 = 4 g R + V C2
e se ora sostituiamo i valori trovati prima per VB e VC otteniamo:
2 g H = 4 g R + g R ---> 2 g H = 5 g R
infine eliminando g troviamo l'altezza "minima" richiesta dal problema:
H = 5/2 R ---> H = 100 cm = 1 m.
![]()
![]()


Inviato da: Enrico Barbarino
il 27/07/2021 alle 18:24
Inviato da: lucky
il 10/09/2013 alle 14:45
Inviato da: Peluche grenouille
il 02/09/2013 alle 08:31
Inviato da: rebel_mc
il 07/02/2013 alle 17:47
Inviato da: carmelo
il 30/01/2013 alle 18:21