GIORNALE DI CLASSEBlog di supporto alle lezioni per gli alunni della Classe Quinta A dell'IPSSAR di Soverato (e non solo) |
LAVORI REALIZZATI DAGLI ALUNNI
MATERIALI DIDATTICI
AREA PERSONALE
MENU
CERCA IN QUESTO BLOG
I MIEI BLOG AMICI
CHI PUÒ SCRIVERE SUL BLOG
I commenti sono moderati dall'autore del blog, verranno verificati e pubblicati a sua discrezione.
| « WEBLOG | LEZIONE DEL 9 MARZO 2007 » |
Asintoti di una funzione.![]()
pag 108 Tomo M.
Definizione di asintoto.
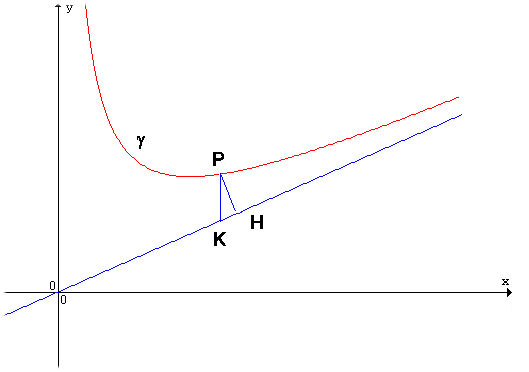
Si dice che la curva g (eventualmente grafico di una funzione di equazione y=f(x)) ammette la retta r come asintoto se la distanza del generico punto P della curva dalla retta r tende a zero quando P si allontana indefinitamente su g.
Affinchè la funzione di equazione y=f(x) abbia l'asintoto obliquo di equazione y=mx+q E' NECESSARIO ( MA NON SUFFICIENTE) che lim x->infinito f(x) = infinito
La funzione di equazione y=f(x) ammette la retta r di equazione y=mx+n come asintoto obliquo SE E SOLO SE valgono le due seguenti proprietà:
- esiste finito il lim per x -> infinito f(x)/x = m
- esiste finito il lim per x ->infinito (f(x) - mx) = n
Il caso delle funzioni razionali fratte
Una funzione razionale fratta (quoziente di due polinomi interi in x) ammette asintoto obliquo SE E SOLO SE il grado del numeratore supera di 1 il grado del denominatore; l'equazione dell'asintoto è y= Q(x), dove Q(x) è il quoziente della divisione del numeratore per il denominatore.
INFO
LINK UTILI
- Risorse di matematica:dienneti
- Risorse di matematica
- Risorse di matematica:edulinks
- Wikipedia.it
- Indire
- Pubblica istruzione
- Esercitazioni on line
- Digiscuola
- Equazioni:un modello della realtà
- Matematicamente
- Test on line:equazioni lineari
- Sistemi in due eq.e due inc.
- Sistemi in tre eq.e tre inc.
- geometria dinamica con cabrì
- Numeri primi e fattorizzazione
- Il gioco del quindici
- Quarto posto -olimpiadi della matematica
- Il giardino di Archimede-un museo per la matematica
- Google
TAG
ULTIMI COMMENTI
Inviato da: Anonimo
il 08/05/2008 alle 16:58
Inviato da: Anonimo
il 23/03/2008 alle 15:58
Inviato da: Anonimo
il 25/12/2007 alle 22:12
Inviato da: Anonimo
il 30/09/2007 alle 17:51
Inviato da: frickpeace
il 25/05/2007 alle 23:07